Fhyujk

Aquest article o secció no cita les fonts o necessita més referències per a la seva verificabilitat.

Mecanisme de quatre barres.

En enginyeria mecànica, un mecanisme de quatre barres o quadrilàter articulat és un mecanisme format per tres barres mòbils i una quarta barra fixa (per exemple, el sòl), unides mitjançant nusos articulats (unions de revoluta o pivots). Les barres mòbils estan unides a la fixa mitjançant pivots. Usualment les barres es numeren de la següent manera:

• Barra 2. Barra que proporciona moviment al mecanisme.


• Barra 3. Barra superior.


• Barra 4. Barra que rep el moviment.


• Barra 1. Barra imaginària que vincula la unió de revoluta de la barra 2 amb la unió de revoluta de la barra 4 amb el terra.

Llei de Grashof

Article principal: Llei de Grashof

La Llei de Grashof és una fórmula utilitzada per analitzar el tipus de moviment que farà el mecanisme de quatre barres: perquè existeixi un moviment continu entre les barres, la suma de la barra més curta i la barra més llarga no pot ser major que la suma de les barres restants.

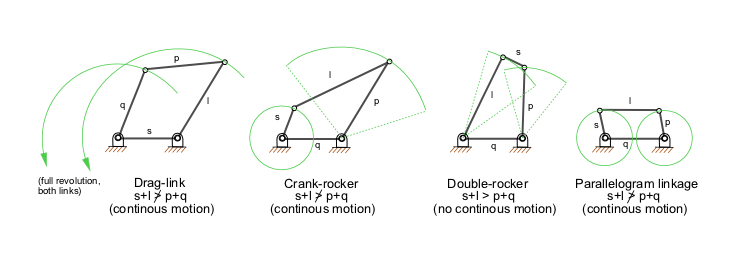
Anàlisi de posició

Per mesures físiques fàcilment es poden tenir les longituds de les barres 1, 2, 3, 4. Ja que la barra 1 és estacionària, el seu angle és fix. Es diu que l'angle de la barra 2 respecte a l'horitzontal és una variable controladora. Per tant, les incògnites són els angles de les barres 3 i 4.

Equació vectorial:

l¯2+l¯3=l¯1+l¯4{displaystyle {bar {l}}_{2}+{bar {l}}_{3}={bar {l}}_{1}+{bar {l}}_{4}}

L2cos⁡θ2i+l2sin⁡θ2j+l3cos⁡θ3i+l3sin⁡θ3j=l1cos⁡θ1i+l1sin⁡θ1j+l4cos⁡θ4i+l4sin⁡θ4j{displaystyle L_{2}cos theta _{2}i+l_{2}sin theta _{2}j+l_{3}cos theta _{3}i+l_{3}sin theta _{3}j=l_{1}cos theta _{1}i+l_{1}sin theta _{1}j+l_{4}cos theta _{4}i+l_{4}sin theta _{4}j}

Separant les equacions en direcció "i" i direcció "j"

Equació en "i": l2cos⁡θ2+l3cos⁡θ3=l1cos⁡θ1+l4cos⁡θ4{displaystyle l_{2}cos theta _{2}+l_{3}cos theta _{3}=l_{1}cos theta _{1}+l_{4}cos theta _{4}}

Equació en "j": l2sin⁡θ2+l3sin⁡θ3=l1sin⁡θ1+l4sin⁡θ4{displaystyle l_{2}sin theta _{2}+l_{3}sin theta _{3}=l_{1}sin theta _{1}+l_{4}sin theta _{4}}

Com es coneixen l'angle de la barra 2 i l'angle de la barra 1, és possible simplificar realitzant els següents canvis de variable:

A=l2cos⁡θ2−l1cos⁡θ1{displaystyle A=l_{2}cos theta _{2}-l_{1}cos theta _{1}}

B=l2sin⁡θ2−l1sin⁡θ1{displaystyle B=l_{2}sin theta _{2}-l_{1}sin theta _{1}}

Amb la qual cosa queda el sistema d'equacions com:

A+l3cos⁡θ3=l4cos⁡θ4{displaystyle A+l_{3}cos theta _{3}=l_{4}cos theta _{4}}

B+l3sin⁡θ3=l4sin⁡θ4{displaystyle B+l_{3}sin theta _{3}=l_{4}sin theta _{4}}

En elevar els termes al quadrat i sumar les dues equacions, tenint en compte que cos2⁡θ+sin2⁡θ=1{displaystyle cos ^{2}theta +sin ^{2}theta =1}, se simplifica de la següent manera:

A2+2Al3cos⁡θ3+B2+2Bl3sin⁡θ3+l32=l42{displaystyle A^{2}+2Al_{3}cos theta _{3}+B^{2}+2Bl_{3}sin theta _{3}+l_{3}^{2}=l_{4}^{2}}

Acos⁡θ3+Bsin⁡θ3=l42−l32−A2−B22l3{displaystyle Acos theta _{3}+Bsin theta _{3}={frac {l_{4}^{2}-l_{3}^{2}-A^{2}-B^{2}}{2l_{3}}}}

És possible tornar a simplificar fent el següent canvi de variable:

C=l42−l32−A2−B22l3{displaystyle C={frac {l_{4}^{2}-l_{3}^{2}-A^{2}-B^{2}}{2l_{3}}}}

Utilitzant les identitats trigonomètriques

sin⁡θ =2tan⁡12θ 1+tan2⁡12θ {displaystyle sin theta ={frac {2tan {frac {1}{2}}theta }{1+tan ^{2}{frac {1}{2}}theta }}}, cos⁡θ =1−tan2⁡12θ 1+tan2⁡12θ {displaystyle cos theta ={frac {1-tan ^{2}{frac {1}{2}}theta }{1+tan ^{2}{frac {1}{2}}theta }}}

i substituint les identitats en l'equació:

A(1−tan2⁡12θ3)+B(2tan⁡12θ3)1+tan2⁡12θ3=C{displaystyle {frac {Aleft(1-tan ^{2}{frac {1}{2}}theta _{3}right)+Bleft(2tan {frac {1}{2}}theta _{3}right)}{1+tan ^{2}{frac {1}{2}}theta _{3}}}=C}

s'obté una equació quadràtica. En utilitzar la fórmula general per resoldre el sistema s'obté:

tan⁡12θ3=B±A2+B2−C2C+A{displaystyle tan {frac {1}{2}}theta _{3}={frac {Bpm {sqrt {A^{2}+B^{2}-C^{2}}}}{C+A}}}

El valor per l'angle de la barra 3 és el següent:

θ3=2tan−1⁡(B±A2+B2−C2C+A){displaystyle theta _{3}=2tan ^{-1}left({frac {Bpm {sqrt {A^{2}+B^{2}-C^{2}}}}{C+A}}right)}

Per obtenir el valor de l'angle de la barra 4 és el mateix procediment, definint el següent canvi de variable:

D=l32−l42−A2−B22l4{displaystyle D={frac {l_{3}^{2}-l_{4}^{2}-A^{2}-B^{2}}{2l_{4}}}}

El valor de l'angle de la barra 4 resulta:

θ4=2tan−1⁡(B±A2+B2−D2D+A){displaystyle theta _{4}=2tan ^{-1}left({frac {Bpm {sqrt {A^{2}+B^{2}-D^{2}}}}{D+A}}right)}

NOTA: els dos valors que es poden obtenir per a cada angle representen les diferents configuracions del sistema.

Anàlisi de velocitat

Aquest mecanisme s'ha d'analitzar mitjançant el mètode de la velocitat relativa

Dades d'entrada

• L'única dada referit a velocitat que es coneix en un mecanisme de quatre barres és la velocitat angular de la barra 2.


• Mitjançant una anàlisi prèvia de posició es coneix la informació de les barres.

Per a l'anàlisi es procedirà a buscar la velocitat del punt B (unió de la barra 3 i 4). Per a aquest punt hi ha dues trajectòries possibles: des O2{displaystyle O_{2},} fins B i des O4{displaystyle O_{4},} fins B. Per començar es defineix la velocitat de B pel que fa a la barra 4

V¯B=ω¯4× l¯4=ω4l4cos⁡θ4j^−ω4l4sin⁡θ4i^{displaystyle {bar {V}}_{B}={bar {omega }}_{4}times {bar {l}}_{4}=omega _{4}l_{4}cos theta _{4}{hat {j}}-omega _{4}l_{4}sin theta _{4}{hat {i}}}

Ara es definirà la velocitat del punt B respecte a l'altra trajectòria.

V¯B=V¯B|A+V¯A=ω¯3× l¯3+ω¯2× l¯2{displaystyle {bar {V}}_{B}={bar {V}}_{B|A}+{bar {V}}_{A}={bar {omega }}_{3}times {bar {l}}_{3}+{bar {omega }}_{2}times {bar {l}}_{2}}

V¯B=ω3l3cos⁡θ3j^−ω3l3sin⁡θ3i^+ω2l2cos⁡θ2j^−ω2l2sin⁡θ2i^{displaystyle {bar {V}}_{B}=omega _{3}l_{3}cos theta _{3}{hat {j}}-omega _{3}l_{3}sin theta _{3}{hat {i}}+omega _{2}l_{2}cos theta _{2}{hat {j}}-omega _{2}l_{2}sin theta _{2}{hat {i}}}

Igualant les equacions per V¯B{displaystyle {bar {V}}_{B},} i separant els components, s'obté un sistema de dues equacions amb dues incògnites.

i^→−ω4l4sin⁡θ4=−ω3l3sin⁡θ3−ω2l2sin⁡θ2{displaystyle {hat {i}}rightarrow -omega _{4}l_{4}sin theta _{4}=-omega _{3}l_{3}sin theta _{3}-omega _{2}l_{2}sin theta _{2}}

j^→ω4l4cos⁡θ4=ω3l3cos⁡θ3+ω2l2cos⁡θ2{displaystyle {hat {j}}rightarrow omega _{4}l_{4}cos theta _{4}=omega _{3}l_{3}cos theta _{3}+omega _{2}l_{2}cos theta _{2}}

Anàlisi d'acceleració

Aquest mecanisme s'ha d'analitzar mitjançant el mètode d'acceleració relativa
les fórmules són:

Simuladors gratuïts

de 4 Barres Gràfica la posició, velocitat i acceleració. (Només per a Windows)

Kima (R) v2.5 Suite de programes per a calcular la posició, velocitat i acceleració dels mecanismes: quatre barres, maneta corredissa i inversió tipus I de maneta corredissa. Funciona en mode interactiu i en mode paramètric, facilitant la interacció amb Matlab (R). Ús lliure per a fins acadèmics.

Vegeu també

• Mecanisme


• Llei de Grashof


• Pantògraf

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Mecanisme de quatre barres